MCS021-DATA AND FILE STRUCTURES | Ignou Solved Question Paper
MCA (Revised) / BCA (Revised) Term-End Examination June, 2015 MCS-021 : DATA AND FILE STRUCTURES
1. (a) Describe the asymptotic notations in detail.
Sol: Use “Big O”, “Omega” and “Theta” notation for asymptotic performance.
Big O notation (Upper Bound):
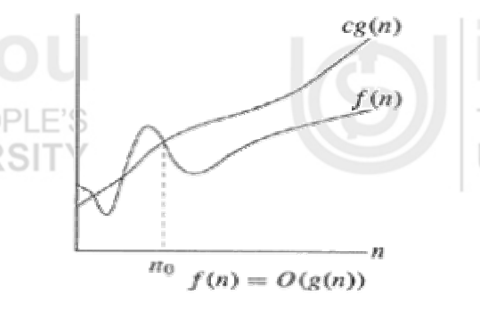
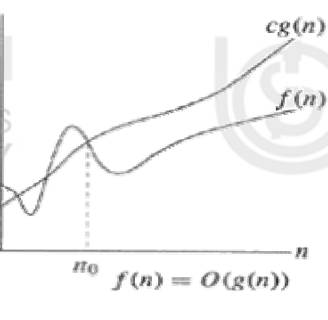
This notation gives an upper bound for a function to within a constant factor. Big O gives an upper bound on the running time of an algorithm. It describes the worst-case time complexity, i.e., the maximum time taken by the algorithm for any input of size n. Figure shows the plot of f(n) = O(g(n)) based on big O notation. We write f(n) = O(g(n)) if there are positive constants n0 and c such that to the right of n0, the value of f(n) always lies on or below cg(n).


The Ω-Notation (Lower Bound)
This notation gives a lower bound for a function to within a constant factor. It describes the best-case time complexity. We write f(n) = Ω(g(n)), if there are positive constants n0 and c such that to the right of n0, the value of f(n) always lies on or above cg(n).
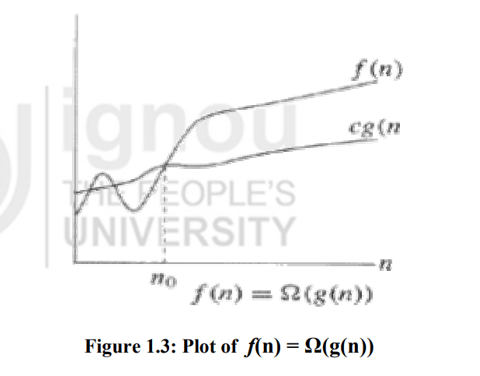
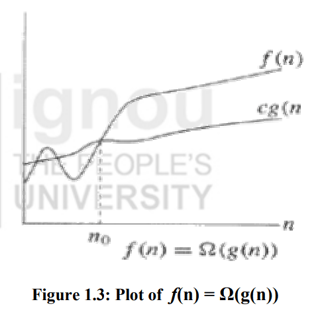
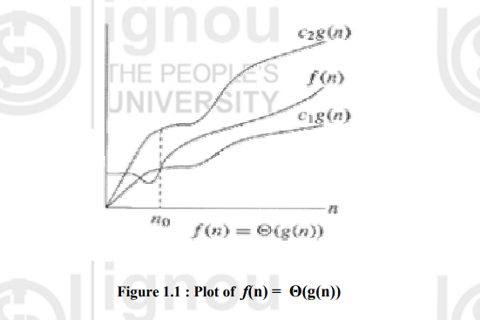
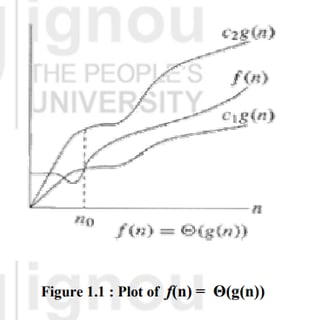
The (Theta)Θ-Notation (Tight Bound)
This notation bounds a function to within constant factors. We say f(n) = Θ(g(n)) if there exist positive constants n0, c1 and c2 such that to the right of n0 the value of f(n) always lies between c1g(n) and c2g(n), both inclusive.
Theta notation provides a tight bound on the running time of an algorithm. It describes both the upper and lower bounds, i.e., the exact growth rate of an algorithm.




(b) Write an algorithm to implement the insertion and deletion operations into a singly linked list
Sol: 🔷 Insertion Operations in a Singly Linked List
1. Algorithm: insertAtFirst()
To insert a node at the beginning of the list:
Create a new node.
If the list is empty:
Set the new node as the Head.
Return.
Set the next pointer of the new node to point to the current Head.
Update the Head to point to the new node.
2. Algorithm: insertAtPosition(pos)
To insert a node at a specific position in the list:
If the position is 0:
Call insertAtFirst() and return.
Initialize:
A counter variable.
A temporary pointer set to the Head.
Traverse the list until you reach the node just before the target position (pos - 1):
Increment the counter during each iteration.
If the temporary pointer becomes NULL before reaching the desired position:
The position is invalid. Return.
Create a new node.
Set the next of the new node to point to the next of the temporary node.
Set the next of the temporary node to point to the new node.
3. Algorithm: insertAtEnd()
To insert a node at the end of the list:
Create a new node.
If the list is empty:
Set the new node as the Head.
Return.
Use a temporary pointer to traverse the list until the last node is reached.
Set the next pointer of the last node to point to the new node.
🔷 Deletion Operations in a Singly Linked List
1. Algorithm: deleteFromFirst()
To delete the first node of the list:
If the Head is NULL:
The list is empty. Return.
Create a temporary pointer and point it to Head.
Update Head to point to the next node.
Set the next of the temporary node to NULL.
Delete the temporary node.
2. Algorithm: deleteFromPosition(pos)
To delete a node from a specific position:
If the Head is NULL, the list is empty. Return.
If the position is 0:
Call deleteFromFirst() and return.
Initialize:
A counter variable.
A temporary pointer to traverse the list.
Traverse the list until reaching the node just before the target position (pos - 1).
If the temporary pointer becomes NULL before reaching the position:
The position is out of bounds. Return.
Store the node to be deleted (i.e., the next of the temporary node) in another pointer.
Update the next of the temporary node to point to the next of the node to be deleted.
Set the next of the node to be deleted to NULL.
Delete the node.
3. Algorithm: deleteFromEnd()
To delete the last node from the list:
If Head is NULL, the list is empty. Return.
If the list has only one node:
Delete the node and set Head to NULL.
Return.
Use a temporary pointer to traverse to the second last node.
Store the last node in another pointer.
Set the next of the second last node to NULL.
Delete the last node.
🔷 Print Operation in a Singly Linked List
Algorithm: printList()
To print all elements in the list:
If Head is NULL, the list is empty. Return.
Set a temporary pointer to the Head.
While the temporary pointer is not NULL:
Print temp->data.
Move temp to temp->next.
// // C Program for Implementation of Singly Linked List
#include <stdio.h>
#include <stdlib.h>
// Define the Node structure
struct Node {
int data;
struct Node* next;
};
// Function to create a new node
struct Node* createNode(int data) {
struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
newNode->data = data;
newNode->next = NULL;
return newNode;
}
// Function to insert a new element at the beginning of the singly linked list
void insertAtFirst(struct Node** head, int data) {
struct Node* newNode = createNode(data);
newNode->next = *head;
*head = newNode;
}
// Function to insert a new element at the end of the singly linked list
void insertAtEnd(struct Node** head, int data) {
struct Node* newNode = createNode(data);
if (*head == NULL) {
*head = newNode;
return;
}
struct Node* temp = *head;
while (temp->next != NULL) {
temp = temp->next;
}
temp->next = newNode;
}
// Function to insert a new element at a specific position in the singly linked list
void insertAtPosition(struct Node** head, int data, int position) {
struct Node* newNode = createNode(data);
if (position == 0) {
insertAtFirst(head,data);
return;
}
struct Node* temp = *head;
for (int i = 0; temp != NULL && i < position - 1; i++) {
temp = temp->next;
}
if (temp == NULL) {
printf("Position out of range\n");
free(newNode);
return;
}
newNode->next = temp->next;
temp->next = newNode;
}
// Function to delete the first node of the singly linked list
void deleteFromFirst(struct Node** head) {
if (*head == NULL) {
printf("List is empty\n");
return;
}
struct Node* temp = *head;
*head = temp->next;
free(temp);
}
// Function to delete the last node of the singly linked list
void deleteFromEnd(struct Node** head) {
if (*head == NULL) {
printf("List is empty\n");
return;
}
struct Node* temp = *head;
if (temp->next == NULL) {
free(temp);
*head = NULL;
return;
}
while (temp->next->next != NULL) {
temp = temp->next;
}
free(temp->next);
temp->next = NULL;
}
// Function to delete a node at a specific position in the singly linked list
void deleteAtPosition(struct Node** head, int position) {
if (*head == NULL) {
printf("List is empty\n");
return;
}
struct Node* temp = *head;
if (position == 0) {
deleteFromFirst(head);
return;
}
for (int i = 0; temp != NULL && i < position - 1; i++) {
temp = temp->next;
}
if (temp == NULL || temp->next == NULL) {
printf("Position out of range\n");
return;
}
struct Node* next = temp->next->next;
free(temp->next);
temp->next = next;
}
// Function to print the LinkedList
void print(struct Node* head) {
struct Node* temp = head;
while (temp != NULL) {
printf("%d -> ", temp->data);
temp = temp->next;
}
printf("NULL\n");
}
// Driver Code
int main() {
struct Node* head = NULL;
insertAtFirst(&head, 10);
printf("Linked list after inserting the node:10 at the beginning \n");
print(head);
printf("Linked list after inserting the node:20 at the end \n");
insertAtEnd(&head, 20);
print(head);
printf("Linked list after inserting the node:5 at the end \n");
insertAtEnd(&head, 5);
print(head);
printf("Linked list after inserting the node:30 at the end \n");
insertAtEnd(&head, 30);
print(head);
printf("Linked list after inserting the node:15 at position 2 \n");
insertAtPosition(&head, 15, 2);
print(head);
printf("Linked list after deleting the first node: \n");
deleteFromFirst(&head);
print(head);
printf("Linked list after deleting the last node: \n");
deleteFromEnd(&head);
print(head);
printf("Linked list after deleting the node at position 1: \n");
deleteAtPosition(&head, 1);
print(head);
return 0;
}
(c) What is a circular queue ? Write an algorithm for insertion and deletion in a circular queue.
Sol: In a circular queue, front will point to one position less to the first element anti-clock wise. So, if the first element is at position 4 in the array, then the front will point to position 3. When the circular queue is created, then both front and rear point to index 1. Also, we can conclude that the circular queue is empty in case both front and rear point to the same index.
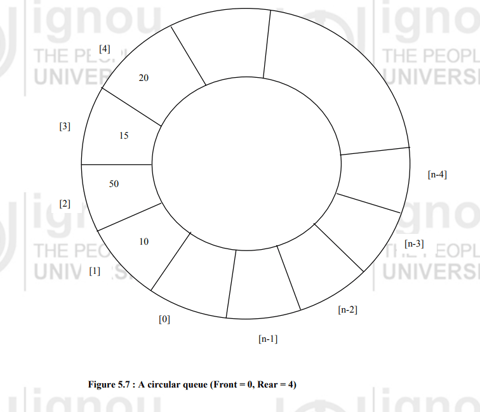
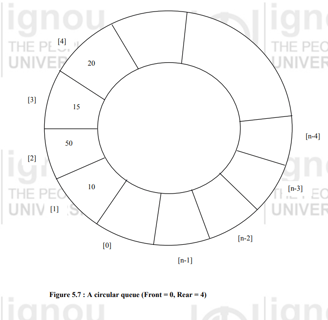
#include “stdio.h”
struct cq
{
int value;
int next;
};
typedef struct cq * cqptr
cqptr p, *front, rear;
main()
{
int choice,x;
/* Initialise the circular queue */
cqptr = front = rear = NULL;
printf (“Enter 1 for addition and 2 to delete element from the queue”)
printf(“Enter your choice”)
scanf(“%d”,&choice);
switch (choice)
{
case 1 :
printf (“Enter the element to be added :”);
scanf(“%d”,&x);
add(&q,x);
break;
case 2 :
delete();
break;
}
}
/************ Add element ******************/
add(int value)
{
struct cq new;
new = (struct cq)malloc(sizeof(queue));
new->value = value new->next = NULL;
if (front == NULL)
{
cqptr = new;
front = rear = queueptr;
} else
{
rear->next = new;
rear=new;
}
}
/* *************** delete element ***********/
delete()
{
int delvalue = 0;
if (front == NULL)
{
printf(“Queue is empty”);
delvalue = front->value;
if (front->next==NULL)
{
free(front);
queueptr = front = rear = NULL;
} else {
front=front->next;
free(queueptr);
queueptr = front;
} } }
(d) Explain the types of rotations performed on AVL trees with an example.
Sol : AVL trees and the nodes it contains must meet strict balance requirements to maintain O(log n) search time. These balance restrictions are maintained using various rotation functions. The four possible rotations that can be performed.
1. Right Rotation (Single Rotation)
Used in: Left-Left (LL) Imbalance
Occurs when a node is inserted into the left subtree of the left child
Example:
Insert in this order: 30 → 20 → 10


Rotation:
Perform Right Rotation on node 30.
2. Left Rotation (Single Rotation)
Used in: Right-Right (RR) Imbalance
Occurs when a node is inserted into the right subtree of the right child.
Example:
Insert in this order: 10 → 20 → 30
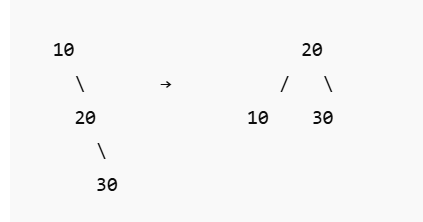
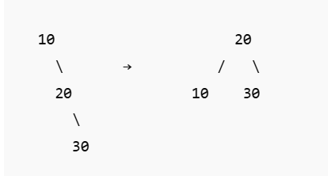
Rotation:
Perform Left Rotation on node 10.
3. Left-Right Rotation (Double Rotation)
Used in: Left-Right (LR) Imbalance
Occurs when a node is inserted into the right subtree of the left child.
Example:
Insert in this order: 30 → 10 → 20
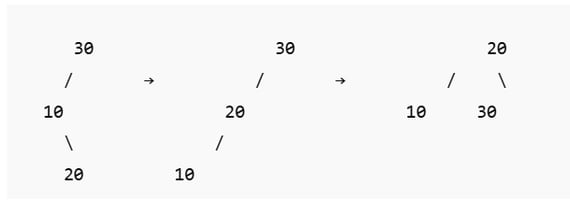
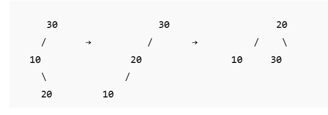
Rotations:
First, Left Rotation on node 10.
Then, Right Rotation on node 30.
4. Right-Left Rotation (Double Rotation)
Used in: Right-Left (RL) Imbalance
Occurs when a node is inserted into the left subtree of the right child.
Example:
Insert in this order: 10 → 30 → 20
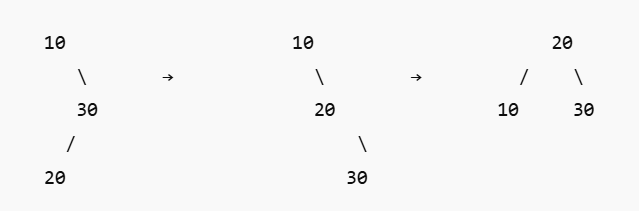
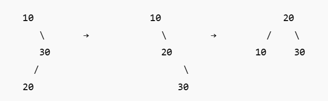
Rotations:
First, Right Rotation on node 30.
Then, Left Rotation on node 10.
2. (a) Write an algorithm to perform each of the following operations :
(i) Insertion of an element into a linear array.
(ii) Delete every third element from a linear array.
Sol:
(i) Insertion of an element into a linear array
Algorithm
Algorithm InsertElement(A, n, item, pos)
Input:
A: linear array of size n
item: the new element to be inserted
pos: position where item is to be inserted (1-based index)
Output:
Array A after inserting item at position pos
1. If n = MAX_SIZE then
Print "Overflow: Cannot insert new element"
Exit
2. If pos < 1 or pos > n + 1 then
Print "Invalid position"
Exit
3. For i ← n - 1 down to pos - 1 do
A[i + 1] ← A[i] // Shift elements to the right
4. A[pos - 1] ← item // Insert item at desired position
5. n ← n + 1 // Increase the size of array
6. Print updated array A[0] to A[n-1]
C Program:
/* Inserting an element into contiguous list (Linear Array) at specified position */
/ contiguous_list.C /
# include
/ definition of linear list /
typedef struct {
int data[10];
int count;
}list;
/prototypes of functions /
void insert(list , int, int);
void create(list *);
void traverse(list );
/ Definition of the insert funtion /
void insert(list start, int position, int element)
{
int temp = start->count;
while( temp >= position) {
start->data[temp+1] = start->data[temp];
temp --;
} start->data[position] = element;
start->count++ ;
}
/* definition of create function to READ data values into the list /
void create(list start) {
int i=0, test=1;
while(test) {
fflush(stdin);
printf("\n input value value for: %d:(zero to come out) ", i);
scanf("%d", &start->data[i]);
if(start->data[i] == 0) test=0;
else i++;
} start->count=i;
}
/* OUTPUT FUNCTION TO PRINT ON THE CONSOLE /
void traverse(list start) {
int i;
for(i = 0; i< start->count; i++)
{
printf("\n Value at the position: %d: %d ", i, start->data[i]);
} }
/* main function */
void main( ) {
int position, element;
list l;
create(&l);
printf("\n Entered list as follows:\n");
fflush(stdin);
traverse(&l);
fflush(stdin);
printf("\n input the position where you want to add a new data item:");
scanf("%d", &position);
fflush(stdin);
printf("\n input the value for the position:");
scanf("%d", &element);
insert(&l, position, element);
traverse(&l);
}
(ii) Delete every third element from a linear array.
Algorithm
Algorithm DeleteEveryThirdElement(A, n)
Input: A linear array A of size n
Output: Array A after deleting every third element
1. Set i ← 2 // Start from the third element (index 2)
2. While i < n do
a. For j ← i to n-2 do
A[j] ← A[j + 1] // Shift elements left to overwrite the i-th element
b. Decrease n ← n - 1 // Reduce array size by 1
c. Set i ← i + 2 // Move to the next 3rd element (adjust for shift)
3. End While
4. Print updated array A[0] to A[n-1]
Step-by Step Explaination :
Example:
Let’s say:
A = [10, 20, 30, 40, 50, 60, 70, 80, 90]
n = 9
Goal: Delete every 3rd element → elements at index 2 (30), 5 (60), and 8 (90) initially.
Step 1: i = 2
Delete A[2] (which is 30), and shift left from index 2:
→ A = [10, 20, 40, 50, 60, 70, 80, 90], n = 8
Update i = 2 + 2 = 4
Step 2: i = 4
Delete A[4] (which is 60), and shift left from index 4:
→ A = [10, 20, 40, 50, 70, 80, 90], n = 7
Update i = 4 + 2 = 6
Step 3: i = 6
Delete A[6] (which is 90), and shift left from index 6:
→ A = [10, 20, 40, 50, 70, 80], n = 6
Update i = 6 + 2 = 8, but since i >= n, stop.
Final Result:
Modified Array: [10, 20, 40, 50, 70, 80]
C Program
#include <stdio.h>
void deleteEveryThird(int arr[], int *n) {
int i = 2; // Start from the 3rd element (index 2)
while (i < *n) {
// Shift elements to the left to overwrite the element at index i
for (int j = i; j < *n - 1; j++) {
arr[j] = arr[j + 1];
}
(*n)--; // Reduce the size of the array
i += 2; // Move to the next 3rd element, considering the shift
}
}
int main() {
int arr[100], n;
// Input array size
printf("Enter the number of elements: ");
scanf("%d", &n);
// Input array elements
printf("Enter %d elements:\n", n);
for (int i = 0; i < n; i++) {
scanf("%d", &arr[i]);
}
// Call the function to delete every third element
deleteEveryThird(arr, &n);
// Print the updated array
printf("Array after deleting every third element:\n");
for (int i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
return 0;
}
(b) Write an algorithm to implement dequeue using array.
Sol: Algorithm to Implement Dequeue Using Array (MCS-021)
Assumptions:
DEQUE[MAX] is an array to store elements.
front and rear are pointers to track the front and rear ends.
Initially, front = -1 and rear = -1.
It can be either input-restricted or output-restricted, but here we assume a general DEQUEUE (insertion and deletion at both ends).
1. Initialize Dequeue
plaintext
CopyEdit
Algorithm Initialize() 1. Set front ← -1 2. Set rear ← -1
2. Insert at Rear
plaintext
CopyEdit
Algorithm InsertRear(DEQUE, item) 1. If rear = MAX - 1 then Print "Overflow at rear" Exit 2. If front = -1 then Set front ← 0 3. Set rear ← rear + 1 4. DEQUE[rear] ← item
3. Insert at Front
plaintext
CopyEdit
Algorithm InsertFront(DEQUE, item) 1. If front = 0 then Print "Overflow at front" Exit 2. If front = -1 then Set front ← 0 Set rear ← 0 3. Else Set front ← front - 1 4. DEQUE[front] ← item
4. Delete from Front
plaintext
CopyEdit
Algorithm DeleteFront(DEQUE) 1. If front = -1 then Print "Underflow" Exit 2. item ← DEQUE[front] 3. If front = rear then Set front ← -1 Set rear ← -1 4. Else Set front ← front + 1 5. Return item
5. Delete from Rear
plaintext
CopyEdit
Algorithm DeleteRear(DEQUE) 1. If rear = -1 then Print "Underflow" Exit 2. item ← DEQUE[rear] 3. If front = rear then Set front ← -1 Set rear ← -1 4. Else Set rear ← rear - 1 5. Return item
6. Display Dequeue
plaintext
CopyEdit
Algorithm Display(DEQUE) 1. If front = -1 then Print "Dequeue is empty" Exit 2. For i ← front to rear do Print DEQUE[i]
Explanation :
A Dequeue allows insertion and deletion from both ends.
We maintain two pointers: front and rear.
Before any operation, we check for overflow and underflow.
This static array-based implementation has limitations, like fixed size and no circular shift.
C Program:
#include “stdio.h”
#define QUEUE_LENGTH 10;
int dq[QUEUE_LENGTH];
int front, rear, choice,x,y;
main() {
int choice,x; front = rear = -1;
/* initialize the front and rear to null i.e empty queue /
printf (“enter 1 for addition and 2 to remove element from the front of the queue");
printf (“enter 3 for addition and 4 to remove element from the rear of the queue");
printf(“Enter your choice”);
scanf(“%d”,&choice);
switch (choice) { case 1: printf (“Enter element to be added :”);
scanf(“%d”,&x);
add_front(x);
break;
case 2:
delete_front();
break;
case 3:
printf (“Enter the element to be added :”);
scanf(“%d ”,&x);
add_rear(x);
break;
case 4:
delete_rear(); break; } }
/*************** Add at the front ***************/
add_front(int y) {
if (front == 0)
{
printf(“Element can not be added at the front“);
return;
else
{
front = front - 1;
dq[front] = y;
if (front == -1 ) front = 0;
} }
/**************** Delete from the front ***************/
delete_front() {
if front == -1 printf(“Queue empty”);
else return dq[front];
if (front = = rear) front = rear = -1 else front = front + 1;
}
/**************** Add at the rear ***************/
add_rear(int y) if (front == QUEUE_LENGTH -1 ) {
printf(“Element can not be added at the rear “) return;
else { rear = rear + 1;
dq[rear] = y;
if (rear = = -1 ) rear = 0;
} }
/**************** Delete at the rear ***************/
delete_rear() {
if rear == -1 printf(“deletion is not possible from rear”);
else {
if (front = = rear) front = rear = -1
else {
rear = rear – 1;
return dq[rear];
} } }
3. (a) Define binary tree. What are the traversals in binary tree ? Explain each traversal with an example
Sol: A binary tree is a special tree where each non-leaf node can have atmost two child nodes. Most important types of trees which are used to model yes/no, on/off, higher/lower, i.e., binary decisions are binary trees.
In a formal way, we can define a binary tree as a finite set of nodes which is either empty or partitioned in to sets of T0, Tl, Tr , where T0 is the root and Tl and Tr are left and right binary trees, respectively.
If a binary tree contains n nodes, then it contains exactly n – 1 edges;
A Binary tree of height h has 2h – 1nodes or less.
If we have a binary tree containing n nodes, then the height of the tree is at most n and at least ceiling log2(n + 1).
If a binary tree has n nodes at a level l then, it has at most 2n nodes at a level l+1
The total number of nodes in a binary tree with depth d (root has depth zero) is N = 20 + 21 + 22 + …….+ 2d = 2d+1 - 1
Three different ways to do the traversal – preorder, inorder and postorder are applicable to binary tree.
In a preorder traversal, the root is visited first (pre) and then the left and right subtrees are traversed. In a postorder traversal, the left sub-tree is visited first, followed by right sub-tree which is then followed by root. In an inorder traversal, the left subtree is visited first, followed by root, followed by right sub-tree
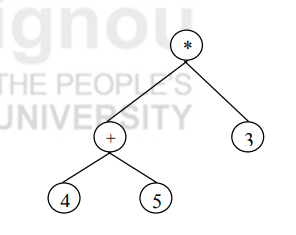
Inoder :
*We are supposed to visit its left sub-tree then visit the node itself and its right sub-tree. Here, root has a left sub-tree rooted at +. So, we move to + and check for its left sub-tree (we are suppose repaeat this for every node). Again, + has a left sub-tree rooted at 4. So, we have to check for 4's left sub-tree now, but 4 doesn't have any left sub-tree and thus we will visit node 4 first (print in our case) and check for its right sub-tree. As 4 doesn't have any right sub-tree, we'll go back and visit node +; and check for the right sub-tree of +. It has a right sub-tree rooted at 5 and so we move to 5. Well, 5 doesn't have any left or right sub-tree. So, we just visit 5 (print 5)and track back to +. As we have already visited + so we track back to . As we are yet to visit the node itself and so we visit before checking for the right sub-tree of , which is 3. As 3 does not have any left or right sub-trees, we visit 3.
So, the inorder traversal results in 4 + 5 * 3
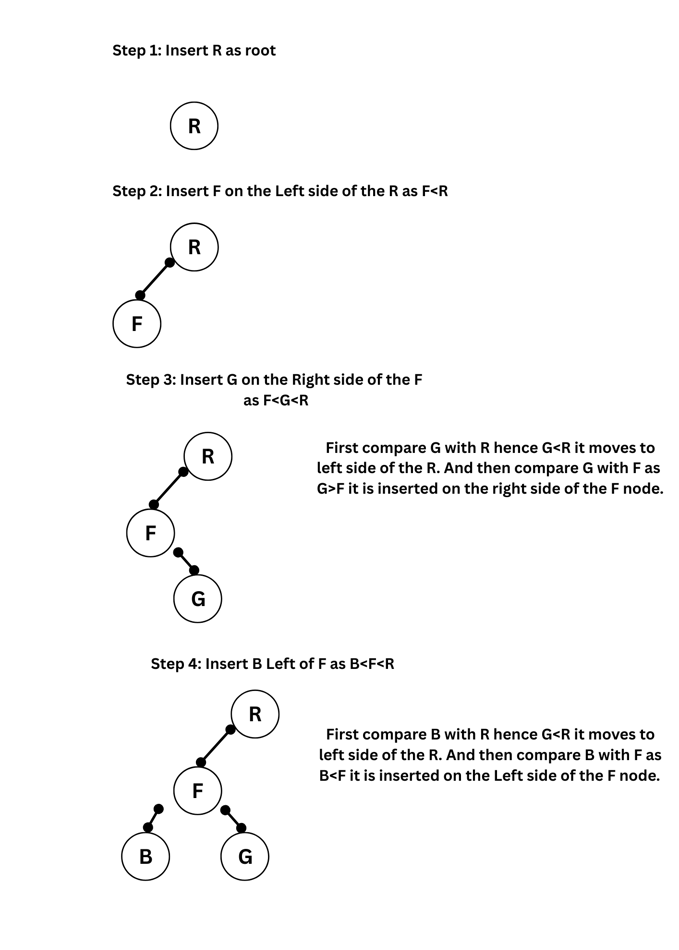
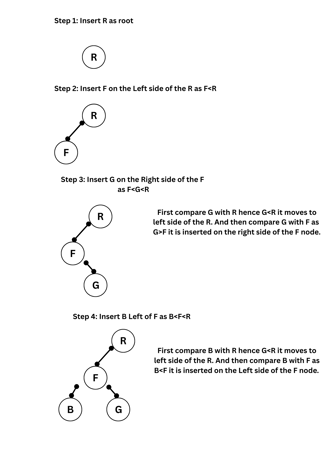
(b) Create a Binary Search Tree for the following alphabets. Start from an empty BST. R, F, G, B, Z, U, P, K, L. Show the trees at each stage.
Sol: While creating a Binary search Tree the first node in inserted and made as root node. The next node is compared and inserted on the left side if it is less than root node and on the right side if it is greater that root node. In the same way the other elements are inserted. which is shown below.
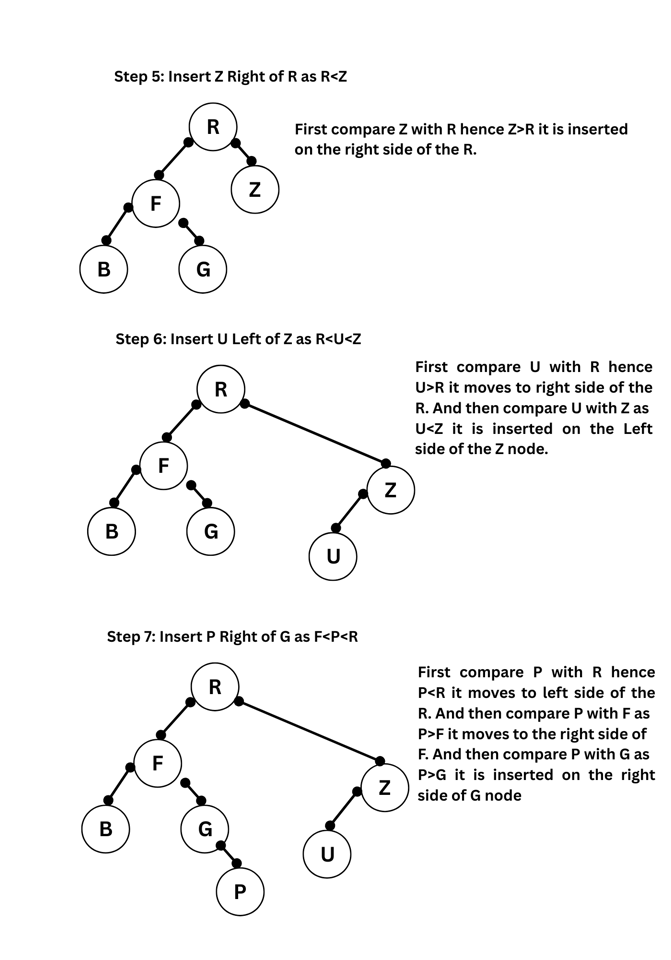
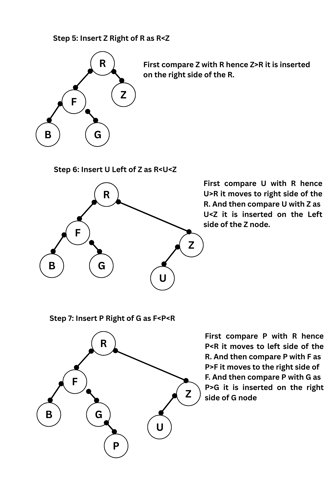
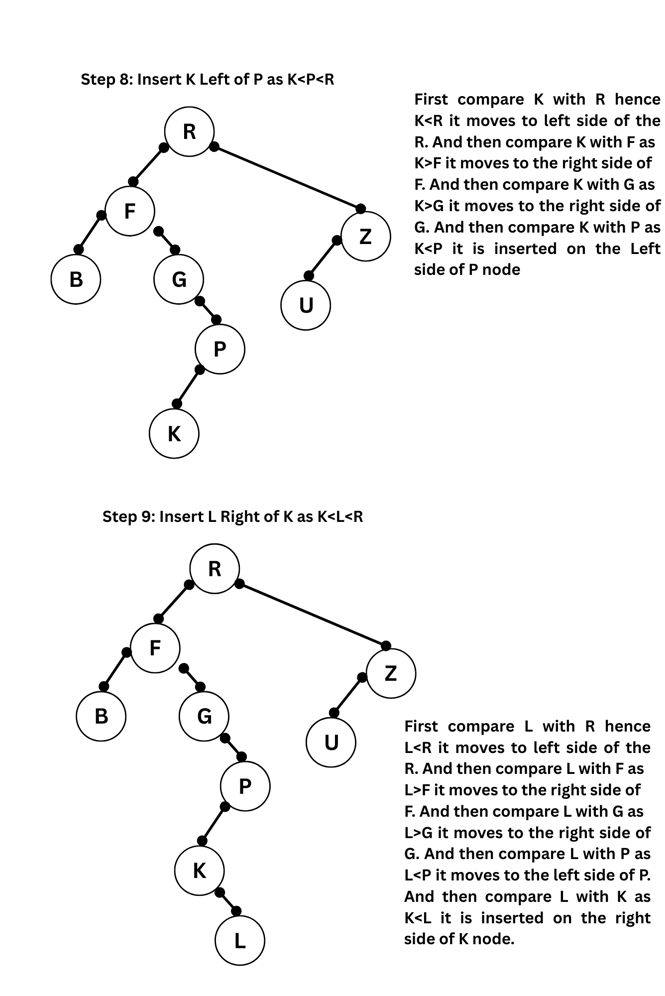
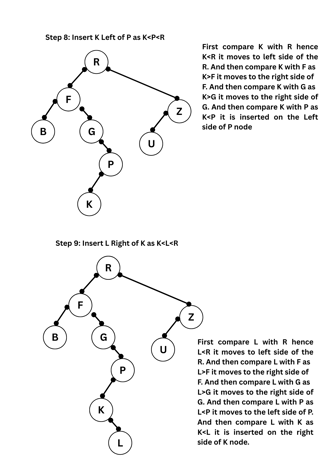
4. (a) Discuss the Prim's algorithm to find the minimum cost spanning tree.
Sol: Prim’s algorithm uses the concept of sets. Instead of processing the graph by sorted order of edges, this algorithm processes the edges in the graph randomly by building up disjoint sets. It uses two disjoint sets A and A. Prim’s algorithm works by iterating through the nodes and then finding the shortest edge from the set A to that of set A (i.e. out side A), followed by the addition of the node to the new graph. When all the nodes are processed, we have a minimum cost spanning tree.
Pseudocode:
1. Initialize MST[] = empty
2. Set key[] = ∞ for all vertices, and parent[] = -1
3. Set key[source_vertex] = 0
4. While MST does not include all vertices:
a. Pick the vertex u with the minimum key value not yet in MST
b. Add u to MST
c. For all adjacent vertices v of u:
If v is not in MST and weight(u,v) < key[v]:
parent[v] = u
key[v] = weight(u,v)
Example:
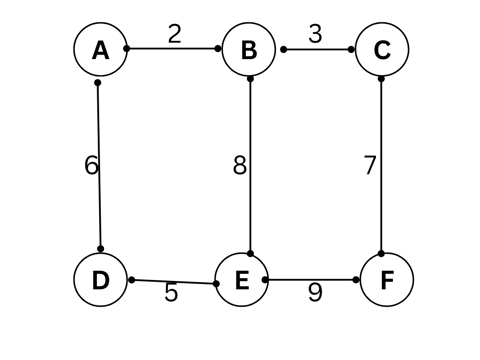
Edges and weights:
AB: 2, AC: 3, AD: 6, BE: 8, CE: 7, DE: 5, EF: 9
Let’s start with A:
Include A
MST = {A}Minimum edge from A: AB = 2
MST = {A, B}From A, B: AC = 3
MST = {A, B, C}From A, B, C: CE = 7, BE = 8 → pick CE = 7
MST = {A, B, C, E}From current nodes: DE = 5
MST = {A, B, C, E, D}Last node F: EF = 9
MST = {A, B, C, E, D, F}
Total Cost of MST = 2 + 3 + 7 + 5 + 9 = 26
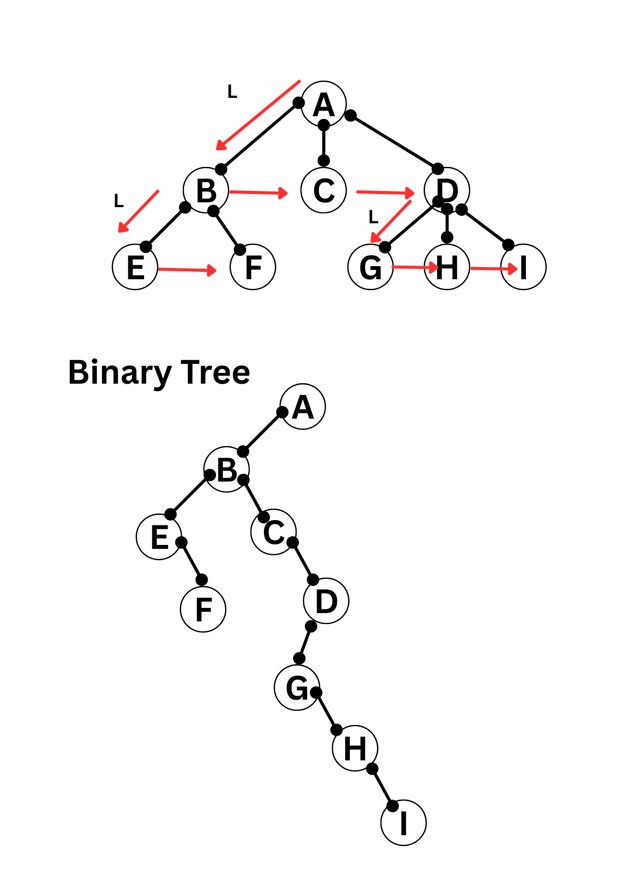
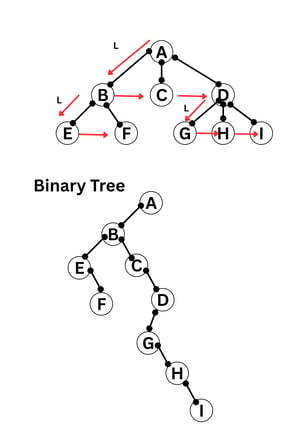
(b) Explain the process of converting a tree to a binary tree.
Sol: steps to convert tree to a binary tree
Step 1: Find branch parent to left most child
Step 2: Connect simbling of each child L to R (Left to Right)
Step 3: Delete all the other links
Step 4: Root of tree is Root of Binary Tree.
Example :
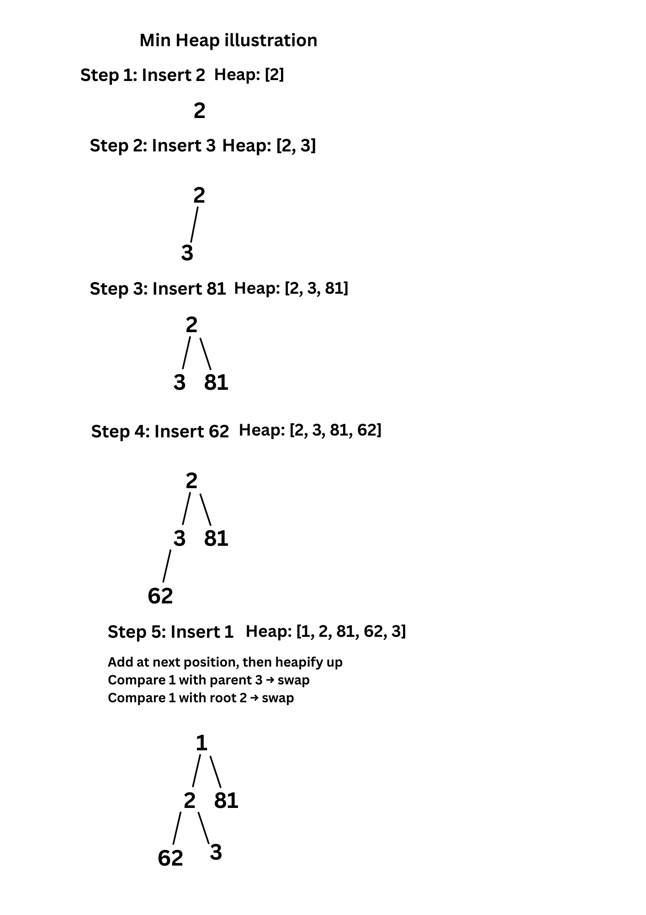
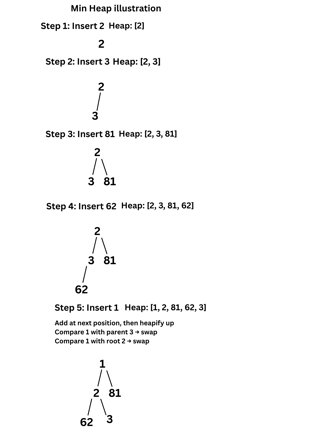
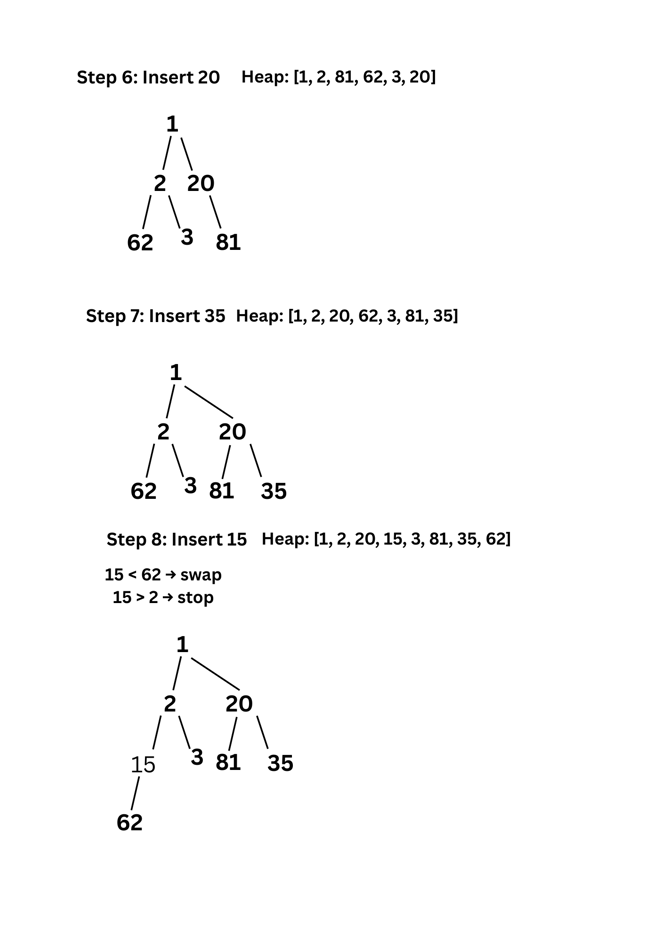
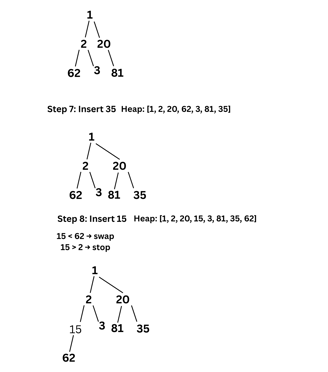
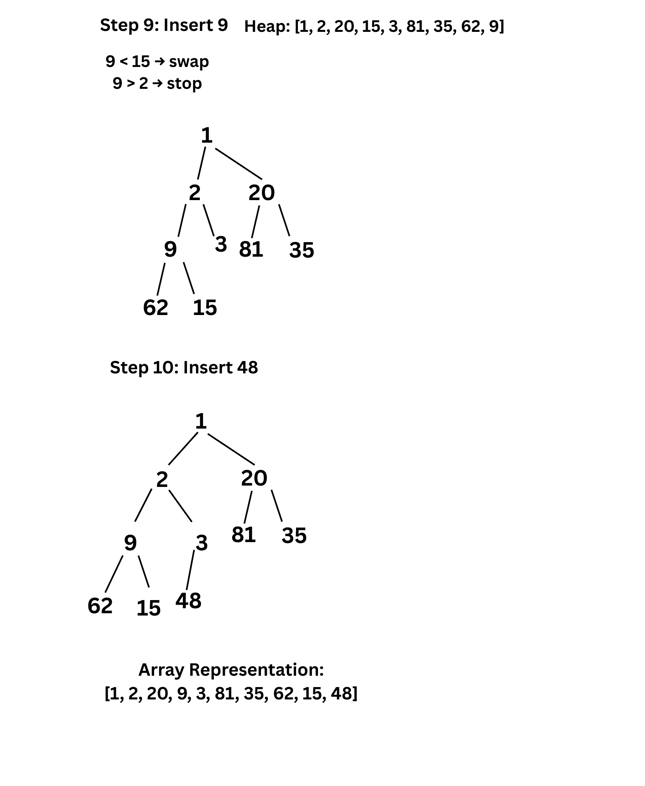
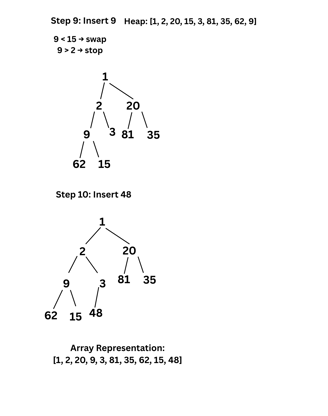
5. (a) Illustrate inserting an element into a heap with the following numbers : 2, 3, 81, 62, 1, 20, 35, 15, 9, 48.
Sol: Below is the illustration of min Heap