MCS021 : Ignou Solved Paper Dec-2016
MCS021 solved question paper December 2016. Ignou previous year solved question papers. BCA solved assignments. Data and File structures complete solved papers.
MCA (Revised) / BCA (Revised)
Term-End Examination December, 2016
MCS-021 : DATA AND FILE STRUCTURES
1. (a) Write an algorithm for multiplication of two matrices.
Sol: Algorithm
Start
Input matrix A
Input matrix B
Initialize result matrix C with all 0s
For each row i in A from 0 to row-1
a. For each column j in B from 0 to col-1
i. Set C[i][j] = 0
ii. For each k
C[i][j] += A[i][k] * B[k][j]Print matrix C
End
C Program :
#include <stdio.h>
int main() {
int A[10][10], B[10][10], C[10][10];
int rows, cols, i, j, k;
// Input rows and columns
printf("Enter number of rows and columns of the matrices: ");
scanf("%d%d", &rows, &cols);
// Input Matrix A
printf("Enter elements of Matrix A (%d × %d):\n", rows, cols);
for (i = 0; i < rows; i++)
for (j = 0; j < cols; j++)
scanf("%d", &A[i][j]);
// Input Matrix B
printf("Enter elements of Matrix B (%d × %d):\n", rows, cols);
for (i = 0; i < rows; i++)
for (j = 0; j < cols; j++)
scanf("%d", &B[i][j]);
// Matrix Multiplication
for (i = 0; i < rows; i++) {
for (j = 0; j < cols; j++) {
C[i][j] = 0;
for (k = 0; k < cols; k++) {
C[i][j] += A[i][k] * B[k][j];
}
}
}
// Output Result
printf("Resultant Matrix (A × B):\n");
for (i = 0; i < rows; i++) {
for (j = 0; j < cols; j++) {
printf("%d ", C[i][j]);
}
printf("\n");
}
return 0;
}
(b) Find the order of the function 3n + 2.
Sol: By looking at the definition of Omega notation and Theta notation, it is also clear that it is of Θ(n), and therefore Ω(n) too. Because if we choose c=1, then we see that cn < 3n+2, hence Ω(n) . Since 3n+2 = O(n), and 3n+2 = Ω(n), it implies that 3n+2 = Θ(n) , too.
(c) Write an algorithm to add two polynomials.
Sol:
#include
void main()
{
int poly1[6][2],poly2[6][2],term1,term2,match,proceed,i,j;
printf("Enter the number of terms in the first polynomial. They should be less than 6:\n");
scanf("%d",&term1);
printf("Enter the number of terms in the second polynomial. They should be less than 6:\n");
scanf("%d",&term2);
printf("Enter the coefficient and exponent of each term of the first polynomial:\n");
for(i=0;i<term1;i++)
{scanf("%d %d",&poly1[i][0],&poly1[i][1]);
}
printf("Enter the coefficient and exponent of each term of the second polynomial:\n");
for(i=0;i<term2;i++)
{scanf("%d %d",&poly2[i][0],&poly2[i][1]);
}
printf(“The resultant polynomial due to the addition of the input two polynomials:\n”);
for(i=0;i<term1;i++)
{
match=0;
for(j=0;j<term2;j++)
{ if (match==0)
if(poly1[i][1]==poly2[j][1])
{ printf("%d %d\n",(poly1[i][0]+poly2[j][0]), poly1[i][1]);
match=1
}}}
for(i=0;i<term1;i++)
{ proceed=1;
for(j=0;j<term2;j++)
{ if(proceed==1)
if(poly1[i][1]!=poly2[j][1])
proceed=1;
else
proceed=0;
} if (proceed==1)
printf("%d %d\n",poly1[i][0],poly1[i][1]);
}
for(i=0;i<term2;i++)
{ proceed=1;
for(j=0;j<term1;j++)
{ if(proceed==1)
if(poly2[i][1]!=poly1[j][1])
proceed=1;
else
proceed=0;
}
if (proceed==1)
printf("%d %d",poly2[i][0],poly2[i][1]);
}}
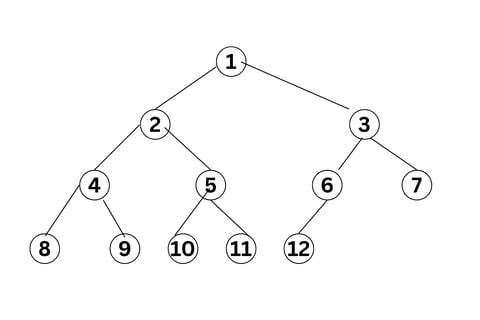
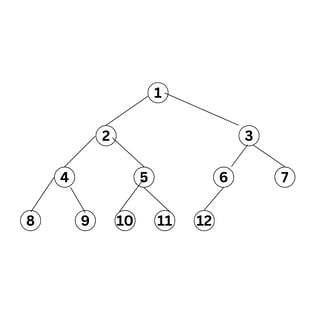
(d) Write the recursive algorithm for various tree traversals. Trace your algorithm for the following data of a Binary Tree : 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
Sol: There are three types of tree traversals, namely, Preorder, Postorder and Inorder.
Algorithm for pre order traversal:
visit root node
traverse left sub-tree in preorder
traverse right sub-tree in preorder
Algorithm for postorder traversal:
traverse left sub-tree in post order
traverse right sub-tree in post order
visit root node
Algorithm for inorder traversal:
traverse left sub-tree
visit node
traverse right sub-tree
Insert the first element as the root.
For subsequent elements, insert them into the next available position in a level-order fashion (e.g., using a queue to keep track of parent nodes).
Example Trace for a Complete Binary Tree with data 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12:
Insert 1: Root = 1
Insert 2: 1.left = 2
Insert 3: 1.right = 3
Insert 4: 2.left = 4
Insert 5: 2.right = 5
Insert 6: 3.left = 6
Insert 7: 3.right = 7
Insert 8: 4.left = 8
Insert 9: 4.right = 9
Insert 10: 5.left = 10
Insert 11: 5.right = 11
Insert 12: 6.left = 12
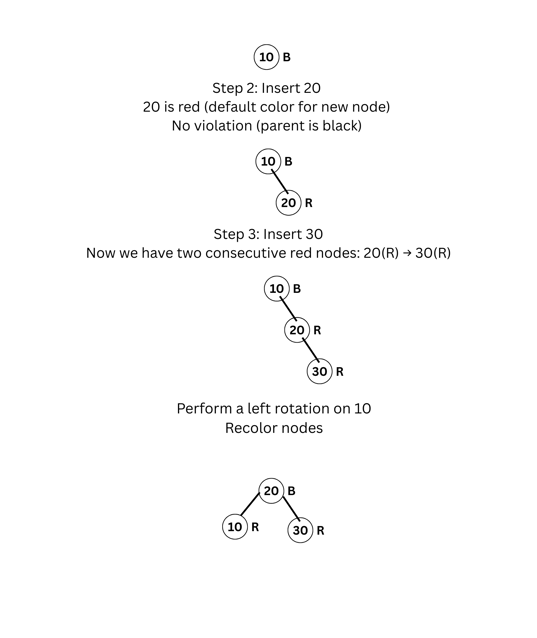
(e) What is a red-black tree ? Explain the properties of a red-black tree with an example.
Sol: A Red-Black Tree (RBT) is a type of Binary Search tree with one extra bit of storage per node, i.e. its color which can either be red or black. Now the nodes can have any of the color (red, black) from root to a leaf node. These trees are such that they guarantee O(log n) time in the worst case for searching. Each node of a red black tree contains the field color, key, left, right and p (parent). If a child or a parent node does not exist, then the pointer field of that node contains NULL value.
Properties of a Red-Black Tree
Each node of a tree should be either red or black.
The root node is always black.
If a node is red, then its children should be black.
For every node, all the paths from a node to its leaves contain the same number of black nodes.
Every leaf which is Nill is Black
If node is Red then its children are Black
Example
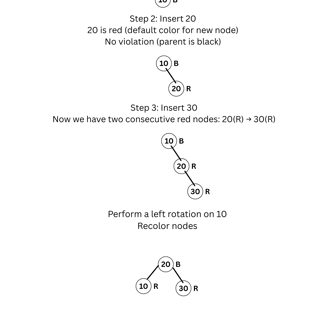
Let's construct a Red-Black Tree by inserting the following values:
10, 20, 30
Step 1: Insert 10
First node is the root ⇒ color it black
10 (b)
2. (a) Write the algorithms for various operations performed on a circular linked list
Sol: The possible operations on a circular linked list are:
Insertion
Deletion
Traversing
Program for Insertion of element
#include
#include
#define
NULL 0
struct linked_list {
int data; struct linked_list *next;
};
typedef struct linked_list clist;
clist *head, *s;
/ prototype of find and insert functions /
clist *find(clist* , int);
clist *insert_clist(clist* );
/definition of insert_clist function /
clist *insert_clist(clist *start) {
clist *n, *n1;
int key, x;
printf("enter value of new element");
scanf("%d", &x);
printf("eneter value of key element");
scanf("%d",&key);
if(start->data ==key)
{
n=(clist* )malloc(sizeof(clist));
n->data=x;
n->next = start;
start=n;
} else {
n1 = find(start, key);
if(n1 == NULL)
printf("\n key is not found\n");
else {
n=(clist*)malloc(sizeof(clist));
n->data=x;
n->next=n1->next;
n1->next=n;
} }
return(start);
}
/*definition of find function /
clist *find(clist *start, int key)
{
if(start->next->data == key)
return(start);
if(start->next->next == NULL)
return(NULL);
else find(start->next, key);
}
void main() {
void create_clist(clist *);
int count(clist* );
void traverse(clist *);
head=(clist *)malloc(sizeof(clist));
s=head;
create_clist(head);
printf(" \n traversing the created clist and the starting address is %u \n", head);
traverse(head);
printf("\n number of elements in the clist %d \n", count(head));
head=insert_clist(head);
printf("\n traversing the clist after insert_clist and starting address is %u \n",head); traverse(head);
}
void create_clist(clist *start) {
printf("inputthe element -1111 for coming oout of the loop\n");
scanf("%d", &start->data);
if(start->data == -1111)
start->next=s;
else {
start->next=(clist*)malloc(sizeof(clist)); create_clist(start->next);
}
}
void traverse(clist *start) {
if(start->next!=s) {
printf("data is %d \t next element address is %u\n", start->data, start- >next);
traverse(start->next);
} if(start->next == s)
printf("data is %d \t next element address is %u\n",start->data, start- >next);
}
int count(clist *start) {
if(start->next == s)
return 0;
else return(1+count(start->next));
}
Program for Deletion of element
#include
#include
#define NULL 0
struct linked_list {
int data;
struct linked_list *next;
};
typedef struct linked_list clist;
clist *head, *s;
/* prototype of find and delete_function*/
clist *delete_clist(clist* );
clist *find(clist* , int);
/*definition of delete_clist /
clist *delete_clist(clist *start) {
int key; clist *f, *temp;
printf("\n enter the value of element to be deleted \n");
scanf("%d", &key);
if(start->data == key) {
temp=start->next;
free(start);
start=temp;
} else {
f = find(start,key);
if(f==NULL)
printf("\n key not fund");
else {
temp = f->next->next;
free(f->next);
f->next=temp;
} }
return(start);
}
/definition of find function /
clist *find(clist *start, int key)
{
if(start->next->data == key)
return(start);
if(start->next->next == NULL)
return(NULL);
else
find(start->next, key);
}
void main() {
void create_clist(clist* );
int count(clist* );
void traverse(clist *);
head=(clist *)malloc(sizeof(clist));
s=head;
create_clist(head);
printf(" \n traversing the created clist and the starting address is %u \n", head);
traverse(head);
printf("\n number of elements in the clist %d \n", count(head));
head=delete_clist(head);
printf(" \n traversing the clist after delete_clistand starting address is %u \n",head);
traverse(head);
}
void create_clist(clist *start) {
printf("inputthe element -1111 for coming oout of the loop\n");
scanf("%d", &start->data);
if(start->data == -1111)
start->next=s;
else {
start->next=(clist*)malloc(sizeof(clist));
create_clist(start->next);
} }
void traverse(clist *start) {
if(start->next!=s)
{
printf("data is %d \t next element address is %u\n", start->data, start- >next);
traverse(start->next);
} if(start->next == s)
printf("data is %d \t next element address is %u\n",start->data, start- >next);
}
int count(clist start)
{
if(start->next == s)
return 0;
else
return(1+count(start->next));
}
(b) Explain the advantages and disadvantages of a Circularly Linked List over a Singly Linked List.
Sol:
1. A Circular Linked List is similar to a Singly Linked List, but with one key difference: the last node’s “next” pointer points back to the first node, creating a circular structure. This looped connection means that traversal can potentially continue indefinitely, making it ideal for applications where elements need to be repeatedly accessed or cycled through.
2.In a Singly Linked List, traversal begins from the head node and continues sequentially to end of the list. It cannot easily be reused for continuous operations.
In a Circular Linked List, the traversal never truly ends because the last node points back to the first node. It is beneficial in situations where continuous looping is desired, such as in a round-robin scheduling algorithm or when implementing a continuous media player playlist.
3.In singly linked list if you need to loop back to the beginning after reaching the end, you’ll need to store an address/reference to the head node. Circular Linked Lists more memory-efficient.
4.Inserting at the end is highly time-consuming. As it requires traversing the entire list to find the last node, making the insertion operation time-consuming (O(n)).
In circulare linked list the last node directly points to the first node so less time consuming, making insertion operations at the end more efficient (O(1)) since you don’t have to traverse the list.
5. Deletion in singly linked list requires finding the second-to-last node. Deletion in circulare linked list is straightforward since last node points to the first.
3. (a) What are the merits and demerits of using pointers over arrays ? Explain
Sol:
